 |
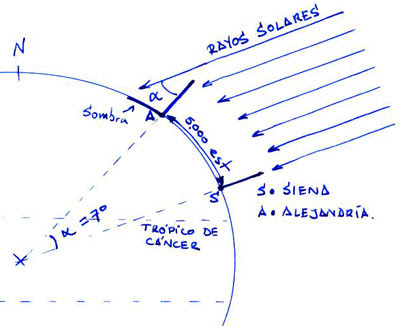
| El cálculo de Eratóstenes |
Es relativamente fácil calcular la latitud. Desde la más remota antigüedad se conocía una interrelación entre la latitud y la declinación de los astros. Eratóstenes fue el primer científico del que tenemos constancia que se percató de este hecho. Aunque culturalmente griego, había nacido en Cirene, una ciudad del antiguo Egipto Ptolemaico en la actual Libia. Eratóstenes comprobó que en Siena (la actual Asuán) una ciudad situada sobre el trópico de Cáncer, que el día del solsticio de verano, al mediodía, los rayos solares caían perpendicularmente al suelo. No producían sombra e iluiminaban el fondo de un pozo profundo. Igualmente se dio cuenta de que en ese mismo momento del año, en Alejandría, una ciudad situada mucho más al norte, esto no ocurría. Al mediodía del solsticio de verano los objetos proyectaban sombra hacia el Norte, y el sol no iluminaba el fondo de los pozos. Dado que los rayos del sol eran paralelos, la única explicación posible a este hecho era que la superficie de la Tierra fuese curva. Eratóstenes midió el ángulo que formaban los rayos solares respecto a la vertical en Alejandría, con un resultado de 7° 12'. Es decir, Alejandría estaba a 7° 12' de latitud Norte respecto a Siena (ya que en Siena los rayos solares formaban un ángulo de 0°) lo que significaba que si perforábamos un pozo en Siena y otro pozo en Alejandría hasta el centro de la Tierra, ambos pozos tendrían entre sí un ángulo de 7° 12'. Por medios que desconocemos (se dice que empleó un regimiento de soldados a los que se ordenó que diesen pasos regulares y los contasen, o que encuestó a los comeriantes de las caravanas entre ambas ciudades) Eratóstenes dedujo que la distancia entre Siena y Alejandría era de 5.000 estadios, y supuso que Alejandría estaba exactamente al norte de Siena (lo cual no es del todo cierto pues en realidad está 3° al Oeste). Con esta distancia y conociendo el ángulo de diferencia, basta un sencillísimo cálculo trigonométrico para calcular el radio terrestre, y todos aprendimos en la escuela (Eratóstenes también) que 2πR = Longitud de la circunferencia, lo que implica que el tomando el arco en radianes, arco = Rα, por lo que Longitud de circunferencia = 2πarco/α. Así, Eratóstenes obtuvo un resultado para la circunferencia de la Tierra de 250.000 estadios. No se sabe qué estadio empleó, ya que en aquella época había muchas medidas que se llamaban "estadio" y en cada sitio tenía un tamaño diferente, como pasaría después con las millas o las leguas, pero dado que él era egipcio, vivía en Egipto, y había estudiado en Alejandría, que era la capital de Egipto, es muy probable que emplease el estadio egipcio, lo que supondría que dio con una circunferencia de la Tierra de 39.614,4 Km. Tan sólo un 1% por debajo de los 40.008 Km de circunferencia media que presenta la Tierra realmente. Como curiosidad diré que Eratóstenes también calculó la distancia de la Tierra al Sol, con un resultado de 804 millones de estadios (139.996.500 Km, cuando la distancia media real es de 149.675.000 Km, un error inferior al 1%) si bien en el cálculo de la distancia a la Luna cometió un error mucho mayor, situándolo más lejos porque sobreestimó el tamaño de nuestro satélite en la creencia de que sería de igual tamaño que la Tierra. Sea como fuere, sigue siendo un misterio cómo pudo realizar mediciones de ángulos tan precisas como para obtener resultados tan asombrosamente perfectos.
El caso es que conocido el tamaño de la Tierra, y sabiendo la fecha, se podía medir la declinación del sol a las 12 del mediodía y en base a unas tablas de efemérides (ya que la declinación del sol en el cénit varía no sólo en función de la latitud, sino también del día del año), viendo la diferencia respecto a la declinación medida sobre el trópico de Cáncer, conocer la latitud. Es decir, saber cuánto al norte o al sur estamos. Así sabemos cuánta distancia hemos recorrido entre dos mediciones, en la dirección Norte-Sur. Sin embargo determinar el desplazamiento en dirección Este-Oeste (la longitud) es más complejo. En tierra firme podemos tomar referencias o puntos fijos, sobre los que establecer la distancia recorrida, lo que nos ofrece una medida de la longitud. Pero en mitad del mar no hay referencias que nos ayuden. Sería de ayuda conocer la velocidad, claro, ya que si conocemos la velocidad y el tiempo que hemos viajado a esa velocidad, podremos calcular la distancia recorrida. Desde antiguo se conocían métodos para determinar la velocidad de un buque, pero no es una velocidad respecto a la superficie terrestre sino respecto al fluido en el que se mueve el barco. Dado que en el agua hay corrientes, navegando a la misma velocidad respecto a tierra, obtendríamos diferentes medidas de velocidad si navegamos a favor o en contra de la corriente (sería como caminar sobre una acera mecánica como las que hay en los aeropuertos, aunque caminemos despacito sobre la acera mecánica, nos movemos muy rápido respecto al aeropuerto, o incluso podemos caminar en contra del movimiento de la acera, con lo que a pesar de estar andando, permaneceremos quietos sobre el mismo punto). En el Mediterráneo, un mar cerrado con corrientes débiles y donde generalmente no se navegaba sin perder de vista tierra fue relativamente fácil calcular la longitud, pero al adentrarse en el Atlántico las cosas cambiaron. Era imposible calcular cuánta distancia sobre la superficie terrestre se había recorrido en un día. Así, por ejemplo, mientras Colón navegó siguiendo escrupulosamente el paralelo de El Hierro, no tenía la menor seguridad de a cuánta distancia estaba de Canarias. De ahí su inseguridad a la hora de determinar su posición y por consiguiente a la hora de dar explicaciones a su tripulación.
Y es que la única forma de medir con exactitud la longitud geográfica (además de contar con un GPS) es disponer de un reloj preciso. Mejor dicho, disponer de dos relojes precisos. La forma ideal de medir la longitud era la siguiente: Se toman dos relojes idénticos, y al inicio del viaje se colocan ambos con la hora solar del puerto de partida. El reloj A permanece con la hora del puerto de partida, mientras que el reloj B se ajusta a las 12:00 cada vez que tenemos el sol en el cénit. Así, si tras 3 días de viaje la diferencia de ambos relojes es de 2 horas y 45 minutos y sabemos que a lo largo de toda la Tierra el desfase es de 24 horas (una rotación de la Tierra dura eso), podemos deducir que hemos recorrido 2,75 horas de las 24 horas que podemos recorrer antes de volver al punto de partida en dirección Este u Oeste. Como cada 24 horas estamos en la misma "hora", y la Tierra gira 360° en cada rotación, cada "hora" de travesía equivale a 15° (360° / 24 = 15), por lo que si hemos recorrido 2,75 "horas", eso son 2,75 × 15° = 41,25° = 41° 15'. Como sabemos que la Tierra tiene 40.000 Km de circunferencia en el ecuador, esto significa que recorrer 360° por el ecuador implica recorrer 40.000 Km, luego por una simple regla de tres recorrer 41° 15' por el ecuador equivale a 4.583 Km. Los paralelos, a diferencia de los meridianos no son todos iguales (el ecuador es mucho más grande que el círculo polar ártico), pero como conocemos con exactitud la latitud, podemos saber cuánto nos hemos movido al Norte o al Sur por lo que con ambas coordenadas, latitud y longitud, sabemos con certeza en qué punto del globo nos encontramos y en qué punto nos encontrábamos ayer, por lo que sabemos la distancia recorrida. Ahora bien, ¿cuál era el problema, si desde la Edad Media se construían relojes? El problema era la precisión. No bastaba tener un reloj sino dos. Y además ambos relojes debían ser exactamente igual de precisos. Como dice el aforismo de Kant "Con un reloj sabes la hora, con dos no estás seguro." Y es que la técnica de relojería distaba mucho de ofrecer una medida precisa del tiempo. Por ello se seguían usando los relojes de sol. El problema es que con un reloj de sol no podía saberse qué hora era en el puerto de origen. No fue hasta bien entrado el siglo XVIII cuando el problema encontró solución. En torno a 1700 había relojes precisos que no atrasaban ni adelantaban y medían el tiempo de forma precisa. El problema era que todos estos relojes eran de péndulo y el movimiento de balanceo de los barcos, así como las condiciones atmosféricas, variación de temperatura, humedad, y la dureza de la travesía alteraban el funcionamiento del reloj lo suficiente para que perdiesen su precisión. Volvíamos a estar en las mismas. En 1714 el Parlamento Británico, consciente del problema que suponía el cálculo de la longitud geográfica tanto para la armada británica como para la marina mercante aprobó la Longitude Act, en la que se dotaba de un premio variable entre 10.000 £ y 20.000 £ de la época (en función de la precisión obtenida) a quien hallase un método fiable para determinar la longitud geográfica. El ganador de este premio fue John Harrison, carpintero de Yorkshire que resolvió el problema mediante la construcción de un reloj lo suficientemente fiable, su cronómetro marino H4. Fabricó sus primeros prototipos en 1730 cuando contaba poco más de 20 años y dedicó por entero su vida a este reto, llegando a fabricar en 1761 relojes que permitían determinar la longitud con menos de medio grado de error. Sin embargo fue necesaria la mediación personal del Rey Jorge III de Inglaterra para persuadir al parlamento de que pagasen a Harrison el premio de 20.000 £ casi diez años después. Los pormenores de la precisión y el funcionamiento del reloj de Harrison excede con mucho el alcance de este artículo, pero sí puede decirse que la genialidad se debió a varios dispositivos inventados por Harrison, como el llamado "péndulo compensado de rejilla", que combinaba barras de hierro y bronce para anular el efecto de la dilatación y contracción debidas a los cambios de temperatura (aunque el H4 no llegó a usar péndulo), el "escape de saltamontes", un sistema para que el reloj liberase la energía del péndulo de forma regular, y casi sin fricción, lo que permitía controlar que prácticamente toda la energía cinética del péndulo se invirtiese en mover las agujas del reloj, o el rodamiento de bolas que conocemos hoy en día, que permitía un movimiento axial con un rozamiento prácticamente nulo.
Prácticamente al mismo tiempo en Francia, tradicional enemigo de Gran Bretaña, Le Roy y Berthoud conseguían otro cronómetro marino de similar precisión y en cuestión de pocos años prácticamente cualquier navío estaba equipado con dos de estos relojes lo que permitió no sólo una navegación más precisa, sino un increíble avance en la cartografía ya que ahora era posible determinar cuánto al este o al oeste estaba determinada isla, determinado cabo, o determinado estuario. Este método de determinar la longitud permaneció vigente hasta después de la Segunda Guerra Mundial, cuando empezó a ser sustituido paulatinamente por la determinación de la posición por radar y posteriormente por el posicionamiento global por satélite o GPS. Hoy podemos calcular la latitud y la longitud con un GPS de uso público con una precisión de 9 millonésimas de grado. Los equipos militares tienen aún más precisión. Si Eratóstenes levantara la cabeza...
Nota: Si has llegado hasta aquí, mándame un correo y házmelo saber. No hay recompensa pero contarás con toda mi admiración.
Enlaces interesantes
Un libro sobre la historia de John Harrison
0 comentarios. Deja alguno tú.:
Publicar un comentario