Otras formas de multiplicar

Multiplicación francesa

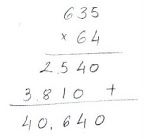
Acaban de pasarme esta página que contiene un interesante vídeo sobre un método para multiplicación que yo no conocía. El caso es que este método me resulta especialmente atractivo por lo gráfico del mismo aunque en esencia no es sino una forma gráfica de hacer una multiplicación por el método de Fibonacci (ver más abajo). Y me he preguntado cuántos profesores de matemáticas lo admitirían como válido. Esta pregunta surge porque el método que la mayoría aprendimos en el colegio para multiplicar números grandes (pongamos 635 x 64) no es más que un convencionalismo. Es decir, no es sino una forma más de resolver esa operación aritmética que llamamos multiplicación. En Matemáticas da bastante igual la forma en la que se llegue al resultado, siempre y cuando el resultado sea correcto. Nuestro método común, llamado "método largo", o "multiplicación francesa" data de finales del s.XVII y consiste en colocar un número bajo otro, y multiplicar el multiplicando por cada una de las cifras del multiplicador, comenzando por la de menor peso, colocando los resultados parciales uno bajo otro, pero desplazándolos un lugar a la izquierda respecto al anterior. Finalmente, se suman los resultados parciales, en nuestro caso 2.540 y 3.810 (que al estar desplazado a la izquierda equivale a 3.810x10=38.100), lo que nos da un resultado de 40.640.

Multiplicación de Fibonacci

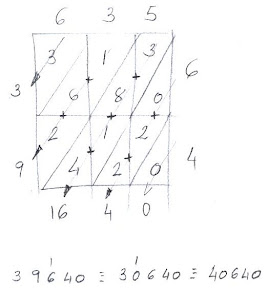
El caso es que este no es ni muchísimo menos el único método posible. Tenemos métodos mucho más divertidos (supongo que por eso no se enseñan en las escuelas), como la "multiplicación con rejilla" o "multiplicación de Fibonacci" (aunque es un método oriental, lo introdujo en Europa Fibonacci en el s.XIII). Consiste en crear una rejilla en la cual, colocaremos en la parte superior el multiplicando, y en el lado derecho el multiplicador, a razón de una cifra por celdilla. Así, en nuestro ejemplo, 635 tiene tres cifras y 64 tiene dos, por lo que la rejilla será de 3x2. A continuación se multiplican los números de las "coordenadas" de cada celdilla, como si jugásemos a los barquitos, pero la celdilla se divide diagonalmente y se colocan las decenas en una mitad y las unidades en la otra. Como 9x9 son 81, nunca nos va a faltar espacio y siempre habrá un dígito en cada mitad de la celdilla. Por último, se suman las diagonales. En nuestro caso tenemos 5 diagonales, (3) (1, 6, 2) (3, 8, 1, 4) (0, 2, 2) y (0). La suma nos da 3, 9, 16, 4 y 0. Si alguna de las sumas diagonales tiene más de un dígito (como ocurre con el 16) las decenas se suman al anterior. En este caso al 9, que nos da 10, lo que hace que repitamos la operación en cadena. Ese 10 queda como 0 y el 1 de las decenas lo sumamos al anterior, el 3, con resultado de 4. Al final tras estos acarreos, las diagonales son 4, 0, 6, 4, 0. El resultado es 40.640.

Multiplicación egipcia

Otro método posible es el llamado “método egipcio”, por ser el comúnmente empleado en el Antiguo Egipto (y a juzgar por el legado arquitectónico, no parece un mal método) si bien es algo complejo ya que lleva implícita una factorización. Consiste en, dados los dos números de nuestro ejemplo 635 y 64. Se hacen dos columnas de números. En la primera doblamos números desde el 1 hasta llegar al multiplicando, o inmediatamente inferior. Es decir, la primera columna, en nuestro caso, sería 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 y no podemos seguir porque el siguiente duplo es 1.024 que es mayor que 635. La siguiente columna estará formada por los duplos del multiplicador, hasta llegar al mismo número de elementos de la primera columna. En nuestro caso sería 64, 128, 256, 512, 1.024, 2.048, 4.096, 8.192, 16.384 y 32.768. El hecho de que los primeros números de esta serie coincidan con los últimos de la anterior es sólo una coincidencia debida a que nuestro multiplicador, el 64, es potencia de 2, pero sólo es una casualidad. El siguiente paso a dar es seleccionar aquellas filas cuyos valores de la primera columna sea igual al multiplicando. Para hallarlo se suma el último valor (siempre va ser uno de las seleccionados) más el anterior. Si nos pasamos (en nuestro caso es así, ya que 512+256=768) desechamos ese valor y seleccionamos el siguiente (en nuestro caso tampoco nos sirve aunque por poquito, ya que 512+128=640) hasta que demos con uno con el que no nos pasemos (en nuestro ejemplo, es el siguiente ya que 512+64=576). Hallado este valor, continuamos sumando este resultado parcial al siguiente (576+32=608, nos sirve), al siguiente, etc., hasta totalizar el multiplicando. En nuestro ejemplo las filas seleccionadas son las que en la primera columna tienen los valores 1, 2, 8, 16, 32, 64 y 512 ya que 1+2+8+16+32+64+512=635, que es nuestro multiplicando. Por último, sumamos los valores no tachados de la segunda columna, cuyo total es el resultado de nuestra multiplicación (32.168+4.096+2.048+1.024+512+128+64=40.640).

Multiplicación rusa

Por último, un método similar aunque más simple, llamado “método del campesino” o “multiplicación rusa”, (o en inglés “russian peasant method”) es otro sistema que en este caso brilla por su sencillez a la hora de aplicarlo ya que sólo requiere saber multiplicar y dividir por dos, cosa que cualquier niño puede hacer de cabeza sin demasiada dificultad. Para aplicarlo, se hace una columna con los sucesivos divisores enteros por 2 del multiplicando. Es decir, 635 entre 2 da 317 con resto 1 (es una división entera). Para este método los restos nos dan igual. Esto lo hacemos sucesivamente hasta llegar al uno. En nuestro ejemplo, la primera columna está compuesta por los elementos 635, 317, 158, 79, 39, 19, 9, 4, 2, 1. En la segunda columna colocamos el multiplicador, y vamos doblándolo sucesivamente de la misma manera que hemos hecho en el método anterior, hasta tener tantos elementos como en la primera columna. Se desechan las filas que tienen un número par en la primera columna, y se suman los que quedan en la segunda columna. Los sumandos, en nuestro ejemplo, puede verse que son los mismos que en el método anterior, y el resultado vuelve a ser 40.640.

No son los únicos métodos para multiplicar, pero creo que con estos ejemplos se aprecia la diversidad de algoritmos que la aritmética posee. En Matemáticas cualquier método es bueno si siempre ofrece resultados correctos. No obstante y por desgracia algunos profesores un tanto estrechos de mente consideran incorrecta la aplicación de cualquier otro método de multiplicación que no sea el que aparece en el programa de estudios.